|
Lassen Sie sich den Artikel vorlesen:
|

In diesem Artikel besprechen wir das Black-Scholes-Modell im Detail und betrachten die Annahmen und Bewertungen, die auf der Formel basieren.
Black-Scholes-Modell
Der Begriff Black and Scholes bezieht sich auf drei Konzepte innerhalb der Finanzmathematik. Wir unterscheiden das Black Scholes-Modell, die partielle Black-Scholes-Differenzialgleichung und die abgeleitete Black Scholes-Formel. Diese Konzepte wurden 1973 von den Wissenschaftlern Fischer Black und Myron Scholes entwickelt.
Das Black & Scholes-Modell ist ein mathematisches Modell für den Finanzmarkt, der Derivate einbezieht. Aus der parabolischen partiellen Differenzialgleichung im Modell, der sogenannten Black-Scholes-Gleichung, kann man die Black Scholes-Formel ableiten. Diese Formel liefert eine theoretische Schätzung des Preises europäischer Optionen. Dieses Modell zeigt auch, dass die Option angesichts des Risikos des Wertpapiers und seiner erwarteten Rendite einen einzigartigen Preis hat.
Kurz gesagt, die oben genannten Personen haben eine Formel entwickelt, mit der Optionspreise berechnet werden können. Später wurde das Modell von Merton weiterentwickelt, weshalb es manchmal auch als Black-Scholes-Merton (BSM)-Modell bezeichnet wird. Für ihre Arbeit erhielt Myron Scholes 1997 den Nobelpreis für Wirtschaftswissenschaften, doch Black war zu diesem Zeitpunkt bereits verstorben.
Annahmen des Black Scholes-Modells
Das Black-Scholes-Modell geht davon aus, dass der Markt aus mindestens einem riskanten Vermögenswert besteht, normalerweise einer Aktie. Darüber hinaus besteht der Markt auch aus einem risikofreien Vermögenswert, beispielsweise Bargeld oder einer Staatsanleihe.
Für den riskanten Vermögenswert werden dann folgende Annahmen getroffen:
- Der Effekt zeigt einen stochastischen Prozess. Das heisst, der Effekt muss die Random-Walk-Theorie erfüllen. Genauer gesagt: die geometrische Brownsche Bewegung (GBM).
- Das betreffende Wertpapier zahlt keine Dividenden.
- Es handelt sich um ein europäisches Derivat, d. h. es gibt nur einen Zeitpunkt, zu dem eine Auszahlung ( Settlement ) erfolgen kann.
Für den „risikofreien“ Vermögenswert (Bargeld oder Staatsanleihe) gehen wir von Folgendem aus:
- Geld kann zu einem gleichbleibenden Zinseszinssatz geliehen und verliehen werden, der über die Zeit konstant bleibt.
- Wir können Aktien für jeden Betrag ohne Handelsgebühren kaufen und verkaufen.
- Möglichkeit, Bargeld in beliebiger Höhe, auch in Bruchteilen, zu einer risikofreien Gebühr zu leihen und zu verleihen.
- Der Markt bietet keine Arbitrage-Möglichkeiten.
Mit dem oben genannten Modell zeigten Black und Scholes, dass es für europäische Call- und Put-Optionen möglich ist, eine abgesicherte Position zu schaffen. Diese Absicherung besteht aus einer Long-Position in der Aktie und einer Short-Position in der Option, deren Wert nicht vom Preis der Aktie abhängt.
Ihre dynamische Absicherungsstrategie führte zu einer partiellen Differenzialgleichung, die den Preis der Option bestimmte. Aus dieser Gleichung leitet sich die Black Scholes-Formel ab.
Bewertung von Optionen mit der Black & Scholes-Formel
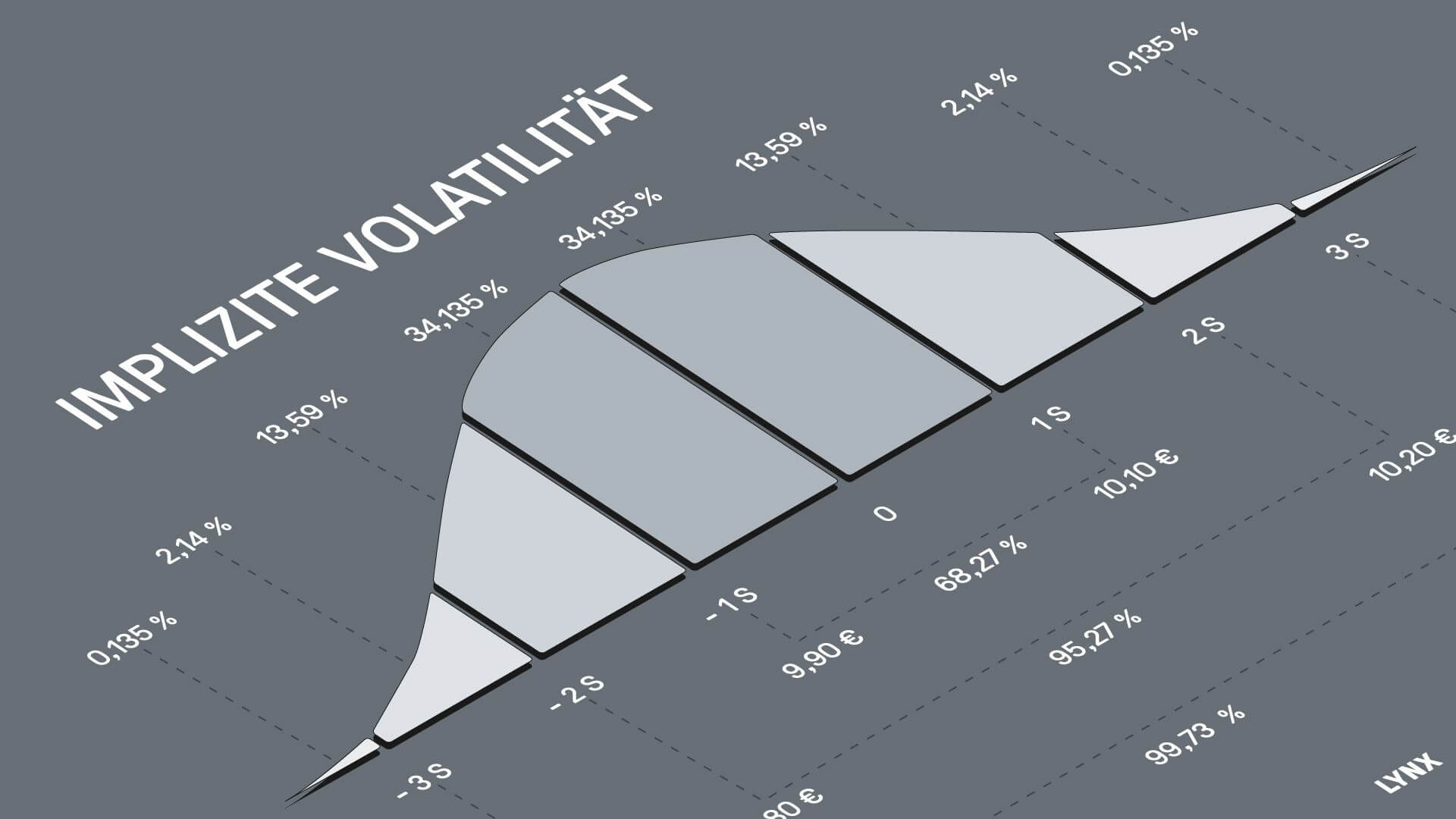
Die Preise von Optionen werden daher nach der Black-Scholes-Formel ermittelt. Die Formel verwendet Aktienkurse, Optionsausübungspreise, Zeit, Volatilität und erwartete Zinssätze. Lediglich die erwartete Volatilität lässt sich nicht direkt am Markt beobachten. Dieser ergibt sich in der Regel aus dem Preis anderer Optionen. Im Folgenden erklären wir kurz die Formel.
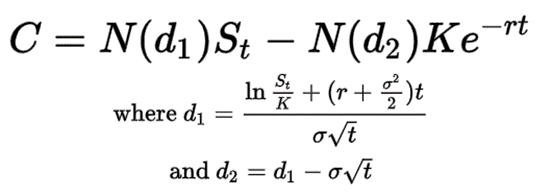
- C = Call-Preis (Preis des Calls)
- N = kumulative Verteilungsfunktion der Normalverteilung
- St = Spotpreis des Vermögenswerts (aktueller Preis)
- K = Ausübungspreis (Strike Price)
- r = risikofreier Zinssatz
- t = Zeit bis zum Ablauf
- σ = Volatilität des Vermögenswerts (Volatilität des Basiswerts)
Welchen Nutzen hat das Black Scholes-Modell für Optionsinvestoren?
Die Bewertung von Optionen ist mittlerweile elektronisch geregelt. Die Optionspreise auf Ihrem Bildschirm werden nach dem Black-Scholes-Modell berechnet. Intelligente Computer berechnen ständig den Wert von Optionen anhand verschiedener Variablen. Dadurch wurde der Optionshandel transparent und für den Privatanleger zugänglich.
Die Kernidee des Modells besteht darin, Optionen durch den Kauf und Verkauf des zugrunde liegenden Vermögenswerts in genau den richtigen Mengen abzusichern und so das Risiko zu eliminieren. Diese Art der Absicherung wird als „kontinuierlich überarbeitete Delta-Absicherung“ bezeichnet und bildet die Grundlage für komplexere Absicherungsstrategien. Diese Strategien sind sehr komplex und werden typischerweise von grossen Investmentbanken und Hedgefonds eingesetzt.
Handel mit Optionen nach dem Black-Scholes-Modell über LYNX
Alles über Optionen:
Volatilität
Griechen